It From Bit

A Brief Exploration of Some Ideas and Results From The Theory Of Computation

(That might appeal to physicists)

By Sahand Saba / sahandsaba.com

Prologue

Assume \(\mathcal{L}\) is some (not necessarily finite, or even countable) set. We are interested in the following two problems:

• Deciding if a given \(x\) is in \(\mathcal{L}\)
• Describing the elements in \(\mathcal{L}\)

Computational Models

To make this accurate we need to make precise two things:

• A mathematical model of computation
• An encoding for \(x\) and \(\mathcal{L}\)

Let's look at the first item for a bit. We will skip the details of encoding for the most part.

Models of Computation

Basic Example

• \(\mathcal{L} = \{x : x \text{ is a binary string and } \mathtt{11} \text{ does not occur in } x\}\)
• For example:
• \(\mathtt{00101} \in \mathcal{L}\)
• \(\mathtt{011} \not\in \mathcal{L}\)

Models of Computation

Finite State Machines

A machine with a finite set of states and transition rules.

For \(\mathcal{L}\) defined on the previous slide:

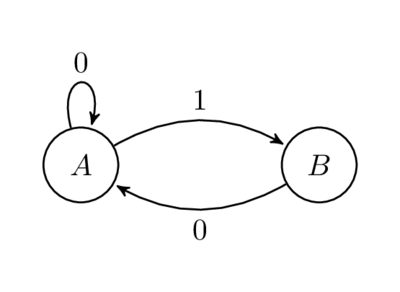
Challange: find the eigen-values of the adjacency matrix for this graph. Do they look familiar? Find how this graph and the associated language \(\mathcal{L}\) is related to the Fibonacci numbers.

Finite State Machines

Limitations

• Very limited.
• Example: \(\mathcal{L}\) the set of binary strings with equal number of ones and zeros.
• Challenge: See if you can prove \(\mathcal{L}\) given above can not be decided using an FSM.

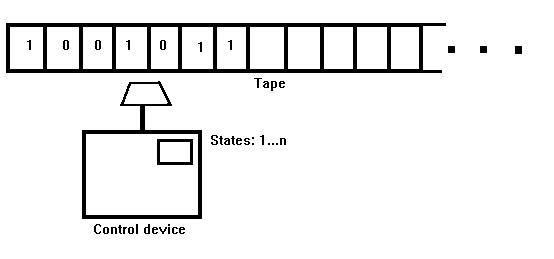
Turing Machines

In simple terms: an FSM that can also read and write to a tape.

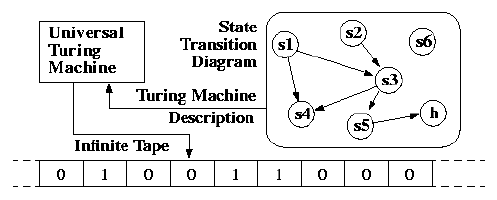
Universal Turing machine

• Input: Description of a Turing machine \(T\) and an input \(x\)
• Output: What \(T\) would output if given \(x\)
• In other words: a Turing machine that "emulates" any given Turing machine

Church-Turing Thesis

• Turing machines turn out to be quite powerful.
• It seems that any meaningful algorithm can be turned into a Turing machine
• This led to the Church-Turing thesis:

Any effectively decidable set \(\mathcal{L}\) can be decided using a Turing machine

• Informally: Turing machines are as good a computing model as we are going to get!

But... How about limitations?

• Let \(\mathcal{L}\) be the set of Turing machines that eventually halt.
• Is \(\mathcal{L}\) decidable using a Turing machine?
• This is known as the Halting Problem
• Equivalent to the following programming assignment:

Write a Python program that reads the source code of another Python program and outputs "yes" if the read program will stop when run, and otherwise "no".

(If you ever teach a first-year programming course and feel devilish, try giving this as an actual assignment to students.)

The Halting Problem

For simplicity, let's go with the Python version.

• Assume such a Python program exists
• Let's say halts_eventually from module magic
• What's the output of the following program?

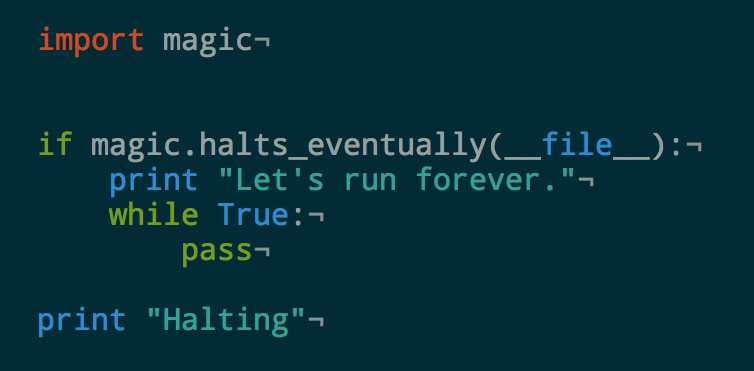
Wait a second...

• Did that idea seem familiar?
• Liar's paradox
• Cantor's proof of \(|A| < |2^A|\)
• Gödel's incompleteness theorems
• Tarski's undefinability of truth
• Incomputability of the Kolmogorov complexity
• etc.

Other Undecidable Problems?

• Set of statements true in number theory (Gödel's incompleteness theorems)
• The group isomorphism problem
• Problems to do with finite simplicial complexes in topology
• Solving Diophantine equations
• Problem of computing the Kolmogorov complexity
• Problems to do with context-free grammars
• Etc...

Turing Complete Problems

Informally, if a system is capable of simulating any Turing machine then the system is said to be Turing complete. Some examples:

• Turing machines (Challenge: might seem obvious, but why?)
• Lambda calculus
• Post tag machines
• Logical gates (AND, OR, NOT)
• Conway's game of life
• Even 1-dimensional cellular automata (rule 110)
• Idealized billiard balls

Game of Life

Simple 2-dimensional cullular automata.

Have a look at this demo.

But billiard balls?

Yes. You can simulate logical gates using them:

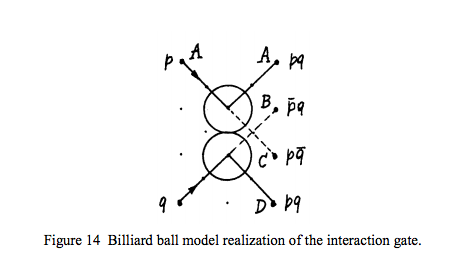
Taken from Fredkin and Toffoli's paper "Conservative logic" (link)

Implications

Many problems to do with Turing complete systems can be inherently so difficult so as to be impossible to solve.

In some sense, this is a "hard" limit on what we can hope to solve computationally.

Kolmogorov Complexity

Given a piece of information (say a string or image), what is the smallest Turing machine (one with the least number of states and transition rules) that can reproduce the information?

This number is defined as the Kolmogorov complexity of the string.

We can replace Turing machine with any Turing complete system. For our examples, let's use Python.

Kolmogorov Complexity

Incomputability

What's the smallest number that can not be described using less than 100 English words?

This paradox is the basic idea behind the proof that Kolmogorov complexity is not computable.

Somewhat related to the "full-employment theorem"... look it up!

Epilogue

Some resources for further exploration

• Turing's "On computable numbers, with an application to the Entscheidungsproblem"
• Godel's "On Formally Undecidable Propositions in Principia Mathematica and Related Systems"
• Hofstadter's "Gödel, Escher, Bach"

Thank you

By Sahand Saba / sahandsaba.com