Introduction

If you are a programmer you are probably a bit sick of the Fibonacci numbers. Code to calculate them is the go-to example for all sorts of situations. This is mostly because the Fibonacci numbers provide one of the simplest examples of a recurrence, making them a good example for any time recursion is part of the discussion. This then makes them a good example for introducing dynamic programming as well. But is that how you would actually calculate them? And the answer is no. Turns out, neither the recursive solution nor the dynamic programming approach are ideal. And no, I am not talking about the closed formula that uses floating point operations to calculate the numbers either. This is a quick post going over the correct way of calculating them. The tl;dr is how to calculate $F_n$ in $O(\log n)$ time, without using any floating point operations. Before presenting the fast algorithm though, I will go through the more well-known solutions first, for the sake of comparison.

The code is intended for Python 3, so range instead of xrange is used, zip is expected to return an iterator, etc. All of it should still run in Python 2, but likely will not be as efficient.

Before we start, here's a quick definition reminder:

and $F_1 = F_2 = 1$ .

Using The Closed Form Formula

Deriving a closed formula for $F_n$ is a simple exercise in solving homogeneous linear recurrences. I skip the details, but if you have never seen the derivation, it is worth looking at. The basic idea is assuming that $F_n = x^n$ for some $x$ , and then solving for $x$ . This means

which implies

Factoring out a $x^{n-2}$ gives

Solving this using the quadratic formula gives

which is where the golden ratio $\phi = \frac{1 + \sqrt{5}}{2}$ comes from. After putting in the initial values and a bit more work, the following formula can be derived:

This can immediately be used to calculate $F_n$ :

from __future__ import division
import math


def fib(n):
    SQRT5 = math.sqrt(5)
    PHI = (SQRT5 + 1) / 2
    return int(PHI ** n / SQRT5 + 0.5)

The Good:

It's fast and simple for small $n$ .

The Bad:

Requires floating point operations. For larger $n$ , more accuracy in floating point operations will be needed. Also, it is no good if we are calculating $F_n$ modulo a number.

The Ugly:

Using irrational numbers to calculate $F_n$ is mathematically beautiful, but from a computer science perspective just ugly.

Recursion

Recursion is perhaps the most obvious solution, and one which you have likely already seen a billion times, most likely as the go-to example of recursion. But here it is again, for the sake of comparison later. We can do it in one line in Python:

fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1

The Good:

Extremely simple implementation, following the mathematical definition.

The Bad:

Exponential running time. Very slow for larger $n$ .

The Ugly:

The stack trace after you get a recursion depth limit error.

Memoization

The recursive solution has a major issue: overlapping recursion subtrees. This is because when fib(n) is called, fib(n-1) and fib(n-2) are calculated. But fib(n-1) in turn will calculate fib(n-2) independently, so fib(n-2) is calculated twice. Continuing in this manner, it is easy to see that fib(n-3) is calculated three times, and so on. So a lot of overlap in the computation.

And here's where memoization comes in. Basic idea is simple: store the results so we don't have to calculate them again. Both time and space complexity of this solution are linear. In the solution below I use a dictionary to do the memoization but a simple list or array could also be used, and would likely be faster if the upper limit of $n$ is known in advance.

M = {0: 0, 1: 1}


def fib(n):
    if n in M:
        return M[n]
    M[n] = fib(n - 1) + fib(n - 2)
    return M[n]

(Python note: you can also do the above using a decorator, for example functools.lru_cache.)

The Good:

Easy to turn a recursive solution to a memoized solution. Will turn previous exponential time complexity to linear complexity, at the expense of more space.

The Bad:

High space complexity to store all previous results and overhead of recursive calls and lookups.

The Ugly:

Same as the recursive solution: the stack trace after you get a recursion depth limit error.

Dynamic Programming

With memoization, it becomes clear that we don't actually need all the previous values stored, just the last two. Also, instead of starting from fib(n) and working backwards recursively, we can start from fib(0) and move forward to reach fib(n). This leads the code below. The running time is linear, but space complexity is now constant. In practise, performance will also be much better since recursive function calls and the branching necessary with the memoization solution are no longer needed. Plus, the code looks much simpler.

This solution is often used as an example of dynamic programming, and is quite well-known.

def fib(n):
    a = 0
    b = 1
    for __ in range(n):
        a, b = b, a + b
    return a

The Good:

Fast for small $n$ , and very simple code.

The Bad:

Still linear number of operations in $n$ .

The Ugly:

Nothing really.

Using Matrix Algebra

And finally, the solution that seems to get the least press, but is the correct one in the sense that it has the best time and space complexity. It is also useful since it can be generalized to any homogeneous linear recurrence. The basic idea here is to use matrices. It is rather simple to see that

Repeated application of the above means that

(Side note: In fact, the two values for $x$ that we got above, one of which was the golden ratio $\phi$ , are the eigenvalues of the matrix above. So using the matrix equation above and a bit of linear algebra would be yet another way of deriving the closed formula.)

All right. So, why is this formulation useful? Because we can do exponentiation in logarithmic time. This is done using a method known as "exponentiation by squaring". I discuss it in a bit more detail in my post on RSA, but the basic recursion is this:

Other than that, we just need to be able to do matrix multiplication and we are set. This leads to the following code. Here I provide a recursive implementation of pow, since it is easier to understand. Feel free to look at the RSA post for an iterative version.

def pow(x, n, I, mult):
    """
    Returns x to the power of n. Assumes I to be identity relative to the
    multiplication given by mult, and n to be a positive integer.
    """
    if n == 0:
        return I
    elif n == 1:
        return x
    else:
        y = pow(x, n // 2, I, mult)
        y = mult(y, y)
        if n % 2:
            y = mult(x, y)
        return y


def identity_matrix(n):
    """Returns the n by n identity matrix."""
    r = list(range(n))
    return [[1 if i == j else 0 for i in r] for j in r]


def matrix_multiply(A, B):
    BT = list(zip(*B))
    return [[sum(a * b
                 for a, b in zip(row_a, col_b))
            for col_b in BT]
            for row_a in A]


def fib(n):
    F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply)
    return F[0][1]

The Good:

Constant space, logarithmic time.

The Bad:

Bit more complicated code.

The Ugly:

Having to deal with matrices, though I personally don't find them that bad.

Performance Comparison

The only two implementations that are worthy of testing are the dynamical programming one and the matrix based one. Thinking in terms of the number of digits of $n$ , the matrix based solution is linear whereas the dynamical programming one is exponential, and that is more or less all that needs to be said. But to see it in practise, here is an example, calculating fib(10 ** 6) which has over two-hundred thousand digits.

n = 10 ** 6
Trying fib_matrix:      fib(n) has 208988 digits, took 0.24993 seconds.
Trying fib_dynamic:     fib(n) has 208988 digits, took 11.83377 seconds.
---

A Graph Theoretic View

This section is a bit of a tangent, and is not directly related to any of the code above. But I find it interesting, so here it is. Consider the graph below.

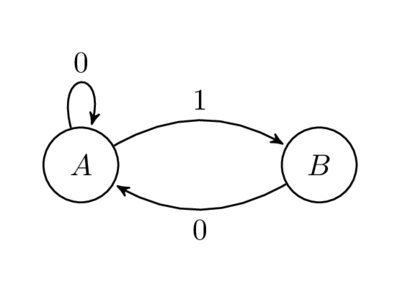
Now, count the number of paths of length $n$ from $A$ to $B$ . For example, for length $n=1$ we have just one path with label sequence $1$ . For $n=2$ we still have just one, but the label is now $01$ . For $n=3$ we have two with labels $001$ and $101$ .

It is a rather simple exercise to show that the number of paths of length $n$ from $A$ to $B$ is in fact precisely $F_n$ . If we write the adjacency matrix of the graph we get the matrix we used in the previous section. It is a well-known basic result in graph theory that given adjacency matrix $A$ , the entries in $A^n$ are the number of paths of length $n$ in the graph. (This was one of the problems in Good Will Hunting, by the way.) So we can provide yet another view of the above methods and formulations.

Why the labels on the edges? Well, turns out that if you consider the infinite sequence of symbols on doubly-infinite paths of the graph, you get what is known as a subshift of finite type which is a type of a symbolic dynamical system. This particular subshift of finite type is known as the "golden mean shift", and is given by the set of forbidden words $\{11\}$ . In other words, we get all doubly-infinite binary sequences with no two ones next to each other. The topological entropy of this dynamical system is the golden ratio $\phi$ . It's interesting to see the number pop up in all sorts of places in mathematics.