Finding Circle Circle Tangents

First, let's focus on finding tangent lines to two disjoint circles. Trust me, this will come in very handy later! Like most geometry and computational geometry problems, vector algebra is going to be very useful in deriving the formulae here, so remember that all points on the plane are treated as vectors in $\mathbb{R}^2$ and the usual vector operations are applicable to them. Also, you can have a look at this JSXGraph applet to get a geometric sense of what we are doing here, although keep in mind that below we derive the tangents purely algebraically, as opposed to the method used in the applet which is a "ruler and compass" construction.

Assume two circles, $C$ and $C'$ are given, with centers at $\vec{o} = (o_x, o_y)$ and $\vec{o'} = (o'_x, o'_y)$ and radii $r$ and $r',$ respectively. Assume the two circles are disjoint and external to each other. Let $\ell$ be a line tangent to both $C$ and $C'$ at points $\vec{p}$ and $\vec{p'}.$ Let $\vec{v} = \vec{p} - \vec{o}.$ Then clearly $|\vec{v}| = r.$ To find the point on the $C'$ corresponding to this tangent, we simply notice that

Hence we can identify the tangent line $\ell$ with the vector $\vec{v}$ since it uniquely identifies a point on $C$ corresponding to the tangent $\ell$ . Note that the choice of $\vec{v'} = +\frac{r'}{r}\vec{v}$ leads to an external tangent line and the choice of $\vec{v'} = -\frac{r'}{r}\vec{v}$ gives an internal one. See figures below.

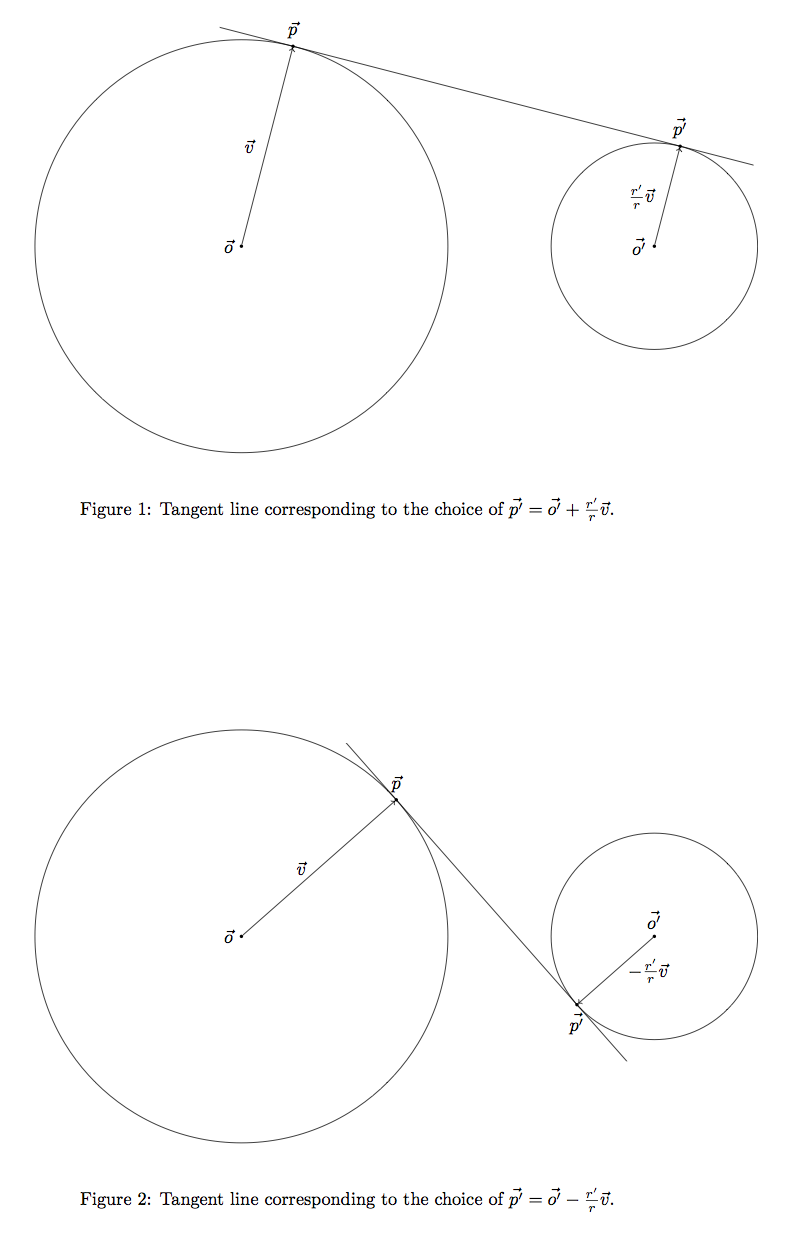
Since $\vec{p} - \vec{p'}$ is on $\ell$ then it is orthogonal $\vec{v}.$ Building on this, we have $\vec{p} - \vec{p'} = \vec{o} + \vec{v} - \vec{o'} - \vec{v'}$ this leads to the following equations:

with $| \vec{v} | = r.$

Assume $\vec{v} = (x, y).$ Then the choice of $\vec{v'} = \frac{r'}{r}\vec{v}$ leads to the following equation in terms of $o_x, o_y, o'_x, o'_y, r$ and $r'$ :

and $\vec{v'} = -\frac{r'}{r}\vec{v}$ gives

Substituting $x^2 + y^2 = r^2$ in these equations simplifies the above to

Let $\mu = o_x-o'_x,$ $\eta = o_y - o'_y,$ and $\delta = r^2 \pm r r',$ with the sign in delta depending on whether we are looking for an internal tangent line or external. Then the equation can be written as

First, assume that $\eta \ne 0.$ Then we can solve for $y,$ getting $y=\frac{-\mu x - \delta}{\eta}.$ Substituting this into $x^2 + y^2 = r^2$ and simplifying gives

which has solutions

provided $\mu^2 + \eta^2 \ne 0,$ which is granted if the circles are not concentric. Now, once we have $x$ we can find $y=\frac{-\mu x - \delta}{\eta}.$

If $\eta = 0$ then $o_y = o'_y$ and we have symmetry along the $x$ -axis. This means that

and for each $x$ we get $y = \pm \sqrt{r^2 - x^2}.$

The above derivation leads directly to the code below to find the tangent lines.

Finding the Line Intersecting Maximal Circles

Now that we know how to find tangents to two circles, let's reduce the circle stabbing problem to the following simpler problem: given a set of disjoint circles $\mathfrak{C} = \{C_1, \ldots, C_n\}$ and a fixed circle $C \in \mathfrak{C}$ find a line $\ell$ that intersects a maximal number of circles in $\mathfrak{C}$ and is tangent to $C.$

For this reduction, it suffices to show that a maximal line can be found that is tangent to at least one circle. Starting with any maximal line $\ell$ we can find a line $\ell$ that intersects the same number of circles as $\ell$ , but is tangent to at least one circle. Let $\vec{n}$ be the normal vector to $\ell$ and let $\ell_\epsilon = \ell + \epsilon \vec{n},$ that is $\ell$ shifted $\epsilon$ units in the direction of its normal. Then for some $\epsilon$ we must have $\ell_\epsilon$ tangent to one of the circles it intersects while still intersecting the same number of circles. Informally, this is because as we increase $\epsilon$ slowly, starting from $\epsilon = 0,$ eventually $\ell_\epsilon$ will intersect fewer circles than $\ell.$ We can pick $\epsilon$ to be immediately before the first drop in the number of circles intersected.

More formally, let $I_\mathfrak{C}(\ell)$ be the number of circles in $\mathfrak{C}$ that $\ell$ intersects. Then we simply let

The above $\epsilon$ is guaranteed to work, for otherwise it is easy to show a contradiction happens.

Given this reduction, we can focus only on lines that are tangent to at least one circle. This gives the following strategy: for each $C \in \mathfrak{C}$ find a line $\ell_C$ that is tangent to $C$ and intersects a maximal number of circles in $\mathfrak{C},$ and find the globally maximal $\ell$ among all the $\ell_C.$ I show that finding the line $\ell_C$ as described here can be achieved in time $O(n \log n)$ and hence finding $\ell$ can be achieved in $O(n^2 \log n)$ time.

To find $\ell_C,$ we observe that given another disjoint circle $C',$ there will be exactly four line tangent to both of them, two internal, and two external. Suppose that an external tangent line to both $C$ and $C'$ goes through point $p^E$ on $C.$ To this external tangent line corresponds an internal one, on the same side of the line connecting the two centers of the circles. Assume the internal tangent intersects $C$ at point $p^I.$ Then for any point $p$ on $C$ that is between $p_E$ and $p_I,$ (here between has to be determined to be clockwise or counter-clockwise based on which side line connect $\vec{o}$ to $\vec{o'}$ the two tangents are) the line tangent to $C$ at $p$ intersects $C'$ as well. Hence we can associate with each pair of corresponding external and internal tangent lines an interval $[p^E, p^I].$

For any $C_k \in \mathfrak{C}$ and $C_k \ne C$ calculate intervals $[p_k^E, p_k^I]$ and $[q_k^I, q_k^E],$ corresponding to the two external/internal tangent line pairs, paying careful attention to the correct order in which they appear in the interval based on a counter-clockwise inclusion, and add both of them to a collection of intervals $Q.$

The problem is now reduced to finding a point $p$ on $C$ that is in a maximal number of intervals in $Q.$ Note that $Q$ has exactly $2(n-1)$ intervals in it.

To find the point $p,$ first for each interval $[p, q] \in Q,$ add the pairs $(Angle(p), 1)$ and $(Angle(q), -1)$ to an array $A.$ Here $Angle(p)$ is to denote the angle the point $p$ makes on the circle $C,$ going counter-clockwise and with the right-most point of $C$ having angle $0,$ and $Angle(q) \in [0, 2\pi).$

Now, sort the elements in $A$ based on their first component, and initialize a variable $c$ with

We now start at angle $\theta = 0$ and simulate moving along $C$ counter-clockwise and keeping track of how many circles the tangent line at angle $\theta$ intersects as we go along. To do this, we use the elements of $A$ as the events, and at each event $a \in A$ we simply set $c \leftarrow c + a[1]$ where $a[1]$ is the second component of $a$ which is equal to $1$ or $-1$ depending on whether the corresponding angle is the beginning of where the tangent lines start intersecting another circle, or the end. We then just need to keep track of the angle $\theta$ where $c$ achieves a maximal value, and voilà, we have $\ell_C$ !

Below is a C++ implementation of the above algorithm. Note that in the code, I ensure that the first pair of external/internal tangents are to the left of the line connecting the centers of $C$ and $C'$ and the second pair to its right. This is needed to ensure the start and end angles are computed correctly, and is done by considering the sign of $\mu$ in the first case and the sign of $\eta$ in the second.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

double EPS = 1e-6;

class Point {
public:
    double x, y;
    Point(double x=0.0, double y=0.0) : x(x), y(y) {}
    double angle() const {
        double a = atan2(y, x);
        if (a < 0) {
            a = atan(1) * 8.0 + a;
        }
        return a;
    }
};

class Event {
public:
    double angle;
    double count;
    Event(double angle = 0, int count = 1) : angle(angle), count(count) {}
    bool operator<(const Event &o) const {
        return angle < o.angle;
    }
};

struct CircleCircleTangents {
public:
    Point external[2];
    Point internal[2];
};

class Circle {
public:
    Point center;
    double radius;
    Circle(double x=0.0, double y=0.0, double r=1.0) : radius(r), center(x,y) {}

    // external[0] and internal[0] are guaranteed to be on the left-side of
    // the directed line connecting C1.center to C2.center
    CircleCircleTangents commonTangents(const Circle& C2) const {
        const Circle& C1 = *this;
        double mu = C1.center.x - C2.center.x;
        double eta = C1.center.y - C2.center.y;
        double r1 = C1.radius;
        double r2 = C2.radius;
        double r1r1 = r1 * r1;
        double r1r2 = r1 * r2;
        double delta1 = r1r1 - r1r2;
        double delta2 = r1r1 + r1r2;
        double D = eta*eta + mu*mu;
        CircleCircleTangents result;
        if (abs(eta) < EPS) {
            // Do not divide by eta! Use x^2 + y^2 = r^2 to find y.
            double dmu = mu < 0? -1 : 1;
            double x = (-delta1 * mu) / D;
            double y = -dmu * sqrt(r1r1 - x * x);
            result.external[0].x = x;
            result.external[0].y = y;
            result.external[1].x = x;
            result.external[1].y = -y;
            x = (-delta2 * mu) / D;
            y = -dmu * sqrt(r1r1 - x * x);
            result.internal[0].x = x;
            result.internal[0].y = y;
            result.internal[1].x = x;
            result.internal[1].y = -y;
        } else {
            // Dividing by eta is ok. Use mu*x + eta*y + delta = 0 to find y.
            double mumu = mu * mu;
            double etaeta = eta * eta;
            double dd1 = delta1 * delta1;
            double dd2 = delta2 * delta2;
            double deta = eta < 0? -1 : 1;
            double Delta1 = deta * sqrt(dd1 * mumu - D*(dd1 - etaeta * r1r1));
            double Delta2 = deta * sqrt(dd2 * mumu - D*(dd2 - etaeta * r1r1));
            double x = (-delta1 * mu + Delta1) / D;
            result.external[0].x = x;
            result.external[0].y = -(mu*x + delta1)/eta;
            x = (-delta1 * mu - Delta1) / D;
            result.external[1].x = x;
            result.external[1].y = -(mu*x + delta1)/eta;
            x = (-delta2 * mu + Delta2) / D;
            result.internal[0].x = x;
            result.internal[0].y = -(mu*x + delta2)/eta;
            x = (-delta2 * mu - Delta2) / D;
            result.internal[1].x = x;
            result.internal[1].y = -(mu*x + delta2)/eta;
        }
        return result;
    }
};

bool add_events(vector<Event>& A, const Point& p, const Point& q) {
    double start = p.angle();
    double end = q.angle();
    A.push_back(Event(start, 1));
    A.push_back(Event(end, -1));
    return start > end;
}

// Given a list of circles, returns (m, c, p) where m is the maximal number of
// circles in C any line can intersect, and p is a point on a circle c in C
// such that the tangent line to c at p intersects m circles in C.
int max_intersecting_line(const Circle* C, int n) {
    int global_max = 1;
    vector<Event> A;
    for(int i = 0; i < n; i++) {
        const Circle& c1 = C[i];
        A.clear();
        int local_max = 1;
        for(int j = 0; j < n; j++) {
            if(j == i) continue;
            const Circle& c2 = C[j];
            CircleCircleTangents Q = c1.commonTangents(c2);
            bool t1 = add_events(A, Q.internal[0], Q.external[0]);
            bool t2 = add_events(A, Q.external[1], Q.internal[1]);
            if(t1 || t2) {
                local_max++;
            }
        }

        if (local_max > global_max) {
            global_max = local_max;
        }

        sort(A.begin(), A.end());
        for(int i = 0; i < A.size(); i++) {
            local_max += A[i].count;
            if(local_max > global_max) {
                global_max = local_max;
            }
        }
    }
    return global_max;
}

int main() {
    Circle C[2000];
    int T;
    cin >> T;
    for (int t = 0; t < T; t++) {
        int n;
        cin >> n;
        for (int i = 0; i < n; i++) {
            cin >> C[i].center.x >> C[i].center.y >> C[i].radius;
        }

        cout << max_intersecting_line(C, n) << endl;
    }
    return 0;
}